Let's have a look at our example images again:

Original 'Lena' image	Original 'Mandrill' image

And here are the above images reduced to 8 colours from the previous article:

'Lena' image reduced to 8 colours	'Mandrill' image reduced to 8 colours

Let's be honest, the colour reduced versions of the originals are hardly great. To improve things we can employ error diffusion which will cause the image to become dithered and give the illusion of more colours than there really are.

Error diffusion works by comparing the actual colour of a pixel against its nearest colour and taking the difference between them which is the error. Portions of this error are then diffused to neighbouring pixels. The simplest form of error diffusion can be shown as:

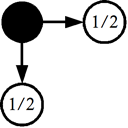
With this form of error diffusion half of the error from the current pixel (represented by the black dot) is diffused to the pixel on the right and half to the pixel below. Please note that the error diffusion should be performed on the red, green and blue components separately.

An important point here is that the total amount of error diffused should never exceed a value of 1. In most cases the total amount of error diffused will equal 1. I am aware of only one type of error diffusion where the total error diffused is less than 1.

It is also important to ensure that when a portion of the error is diffused to neighbouring pixels it does not cause invalid values, e.g. go below 0 or above 255. Should a value go outside of the valid range then it should be truncated.

Here is some pseudo-code for the simple error diffusion which should be performed after the current pixel at x,y has been changed to the nearest colour:

   error = actualColour - nearestColour
   PutPixelColour(x+1, y  ) = Truncate(GetPixelColour(x+1, y  ) + 0.5 * error)
   PutPixelColour(x  , y+1) = Truncate(GetPixelColour(x  , y+1) + 0.5 * error)

The procedure Truncate() in pseudo-code:

   Procedure Truncate(value)
      If value < 0 Then value = 0
      If value > 255 Then value = 255
      Return value
   EndProcedure

The quality of this type of error diffusion however is pretty poor and very few people would actually use it. A better one, and arguably the most famous, is Floyd-Steinberg error diffusion. This can be shown as follows:

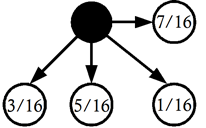
With Floyd-Steinberg error diffusion the error is distributed amongst more neighbouring pixels providing a much nicer overall dithering effect. Here is the Floyd-Steinberg error diffusion in pseudo-code:

   error = actualColour - nearestColour
   PutPixelColour(x+1, y  ) = Truncate(GetPixelColour(x+1, y  ) + 7/16 * error)
   PutPixelColour(x-1, y+1) = Truncate(GetPixelColour(x-1, y+1) + 3/16 * error)
   PutPixelColour(x  , y+1) = Truncate(GetPixelColour(x  , y+1) + 5/16 * error)
   PutPixelColour(x+1, y+1) = Truncate(GetPixelColour(x+1, y+1) + 1/16 * error)

Performing the colour reduction with Floyd-Steinberg error diffusion will produce the following results:

'Lena' image reduced to 8 colours with error diffusion	'Mandrill' image reduced to 8 colours with error diffusion

As a comparison here are zoomed close-ups of the Lena images:

Zoomed close-ups of the original, colour reduced and dithered Lena images

Despite having the same palette I am sure you will agree the colour reduced images with error diffusion look a lot better than the standard colour reduced images.

Programs written to accompany this series demonstrating the techniques discussed are available from here. There are versions of the programs available for Linux, Mac OS X and Windows platforms. Please be sure to read the 'readme.txt' files for more information.

Amiga Roundtable Podcast